TP2: Simulation de lois élémentaires

Objectifs de ce TP
  • Utiliser les générateurs aléatoires en Python et numpy, savoir afficher un histogramme, une densité, etc.
  • Comprendre au mieux comment utiliser les fonctions aléatoires (principalement les générateurs) en numpy.

Loi uniforme et graine

Avec numpy, la fonction numpy.random.uniform permet la génération de réalisations pseudo-aléatoires de la loi uniforme sur [0,1].

On peut modifier la taille de l’échantillon généré en modifiant l’argument de la fonction. Pour obtenir n=4 réalisations i.i.d. de loi uniforme, essayez par exemple

import numpy as np
np.random.uniform(size=4)
array([0.19976872, 0.79296023, 0.96855398, 0.66943824])

Pour rappel, l’algorithme de génération de v.a. est récursif et s’appuie sur une graine. La graine peut être modifiée avec la création d’un générateur, et il suffit d’entrer un nombre en argument pour fixer cette graine.

rng = np.random.default_rng(seed=34)
print(rng.uniform())
rng = np.random.default_rng(34)
print(rng.uniform())
0.004028243493043537
0.004028243493043537

Changer les valeurs de seed et vérifier que les tirages ont bien changé.

Exercice 1: Simulation de loi uniforme et histogramme

Créez un vecteur de taille 1000 composé de réalisations i.i.d. de v.a.uniformes sur [-1,1]. Dans la suite on supposera que l’on a chargé matplotlib pour l’affichage graphique avec la commande:

import matplotlib.pylab as plt
from scipy import stats

À l’aide de la fonction plt.hist, représentez l’histogramme de cet échantillon.

Solution

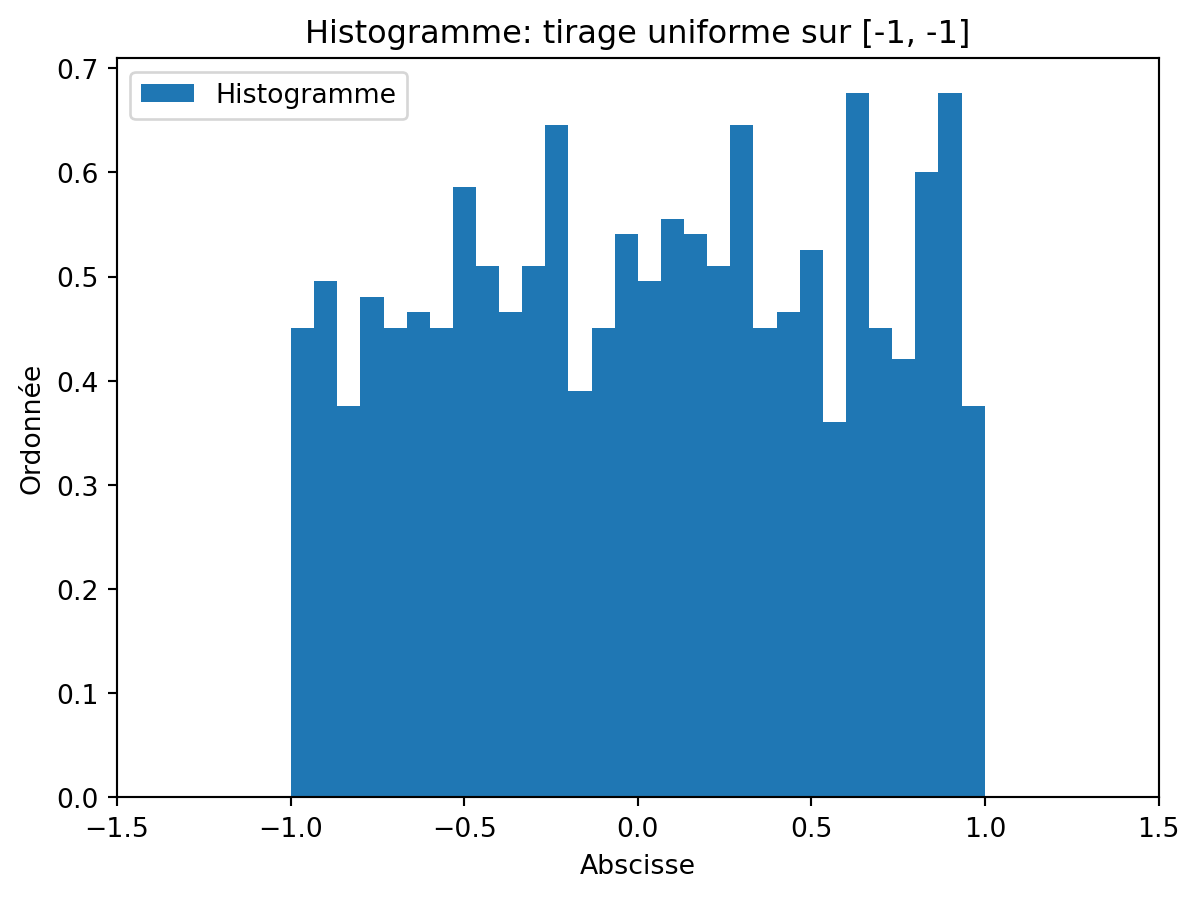
fig, ax = plt.subplots()
vect = rng.uniform(-1, 1, 1000)
ax.hist(vect, label="Histogramme", bins=30, density=True)
plt.title("Histogramme: tirage uniforme sur [-1, 1]")
plt.legend()
ax.set_xlim((-1.5,1.5))
ax.set_xlabel('Abscisse')
ax.set_ylabel('Ordonnée')
plt.show()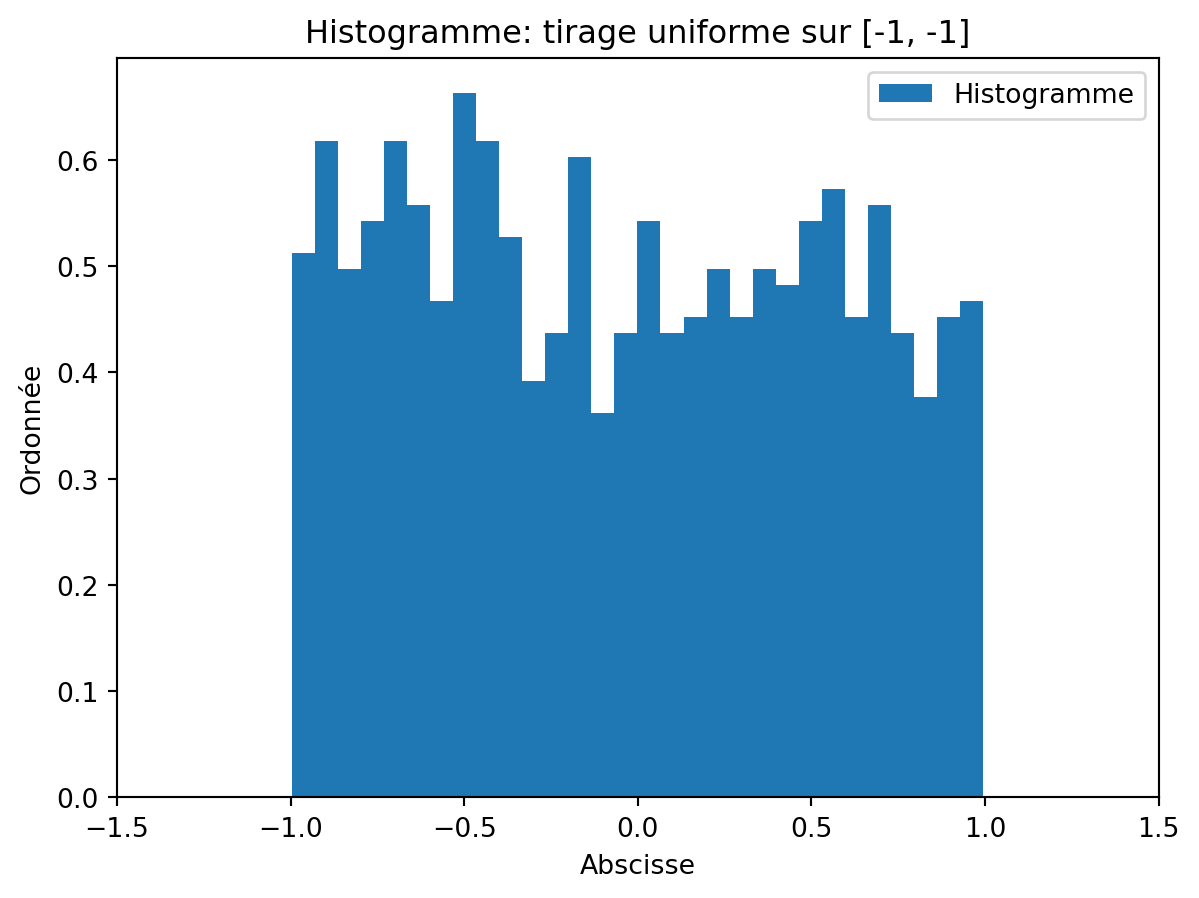

On utilisera l’aide de hist de matplotlibs pour préciser les options graphiques suivantes:

  • Analysez en particulier ce que fait l’option bins en entrant l’option bins=30 et bins=10.
  • Modifiez également votre histogramme avec l’option density=True, de sorte que l’aire soit de 1 (on représente donc une densité qui est constante par morceaux)
  • Ajoutez un titre à l’histogramme grâce à la commande plt.title (avec une chaîne de caractères entre guillemets). On peut également ajouter un nom aux axes avec l’option plt.xlabel et plt.ylabel.
  • Les options ax.set_xlim et ax.set_ylim permettent de préciser l’échelle de axes: il faut préciser un tuple (a,b) où a<b sont les deux bornes choisies pour votre axe.
  • On modifiera aussi les options fill et histtype de hist pour obtenir le résultat suivant, en affichant sur un même graphique trois tirages, de tailles 1000, 5000 et 10000.
  • La densité de la loi uniforme est obtenue avec la fonction pdf du module scipy.stats. Créer un vecteur équiréparti sur [-2, 2] de longueur 300 évaluer la fonction sur la même figure: on souhaite superposer cette densité à l’histogramme. On utilisera la fonction plot pour tracer la densité, et on pourra utiliser l’option alpha pour rendre la densité plus transparente.

Un exemple de figure de qualité acceptable est par exemple celle qui suit:

Solution

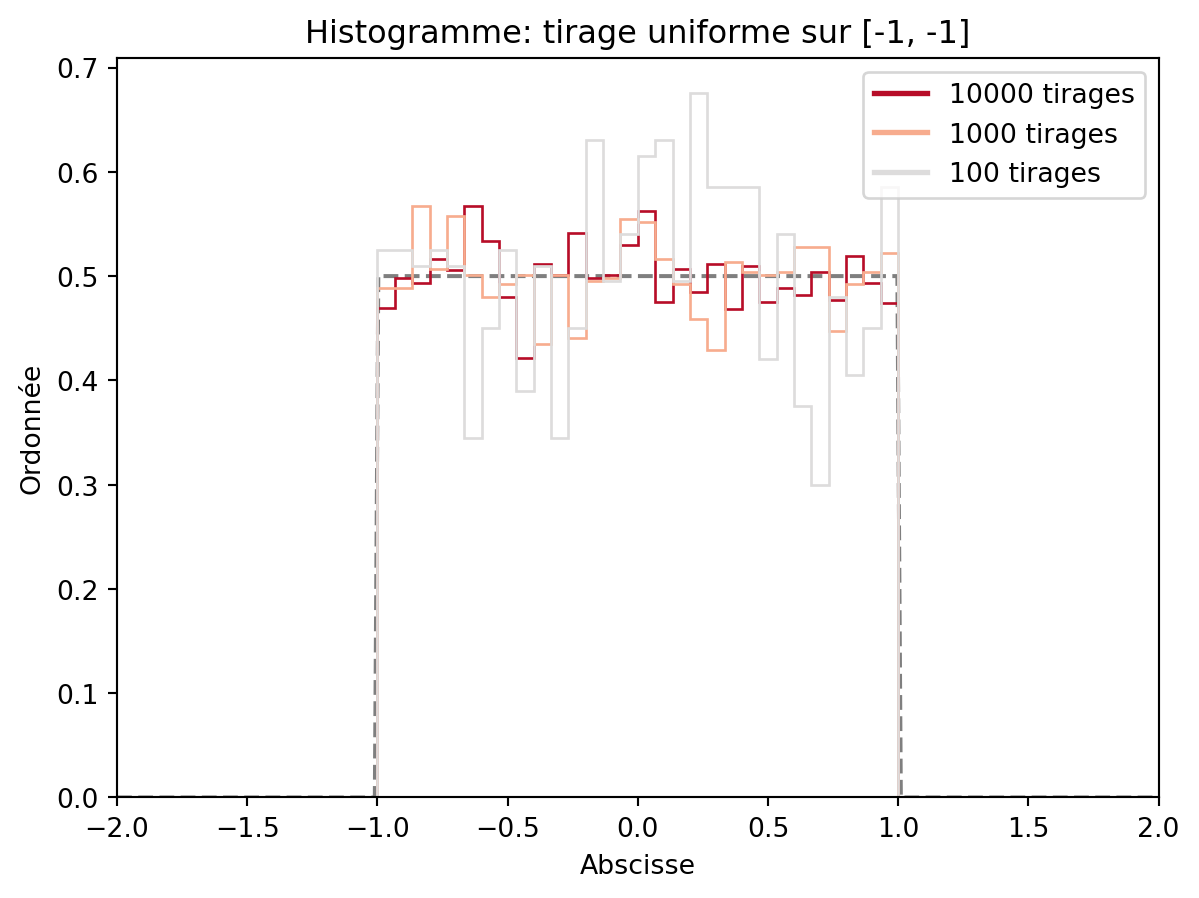
cmap = plt.cm.coolwarm
vect100 = rng.uniform(-1, 1, 1000)
vect1000 = rng.uniform(-1, 1, 5000)
vect10000 = rng.uniform(-1, 1, 10000)
x = np.linspace(-2, 2, num=300)

fig, ax = plt.subplots()
colors=[cmap(0.99), cmap(0.7), cmap(0.5)]

ax.plot(x, stats.uniform.pdf(x, loc=-1,scale=2),'--', color='k', label="Loi théorique", alpha=0.5)

ax.hist(vect10000, histtype='step', density=True, bins=30, label="Histogramme 10000", fill=False, color=colors[0])
ax.hist(vect1000, histtype='step', density=True, bins=30, label="Histogramme 5000", fill=False, color=colors[1])
ax.hist(vect100, histtype='step', density=True, bins=30, label="Histogramme 1000", fill=False, color=colors[2])

plt.title('Histogramme: tirage uniforme sur [-1, 1]')
plt.xlabel('Abscisse')
plt.ylabel('Ordonnée')

ax.set_xlim((-2,2))

from matplotlib.lines import Line2D

custom_lines = [Line2D([0], [0], color=colors[0], lw=2),
                Line2D([0], [0], color=colors[1], lw=2),
                Line2D([0], [0], color=colors[2], lw=2)]

ax.legend(custom_lines, ['10000 tirages', '1000 tirages', '100 tirages'], loc='upper right')

plt.show()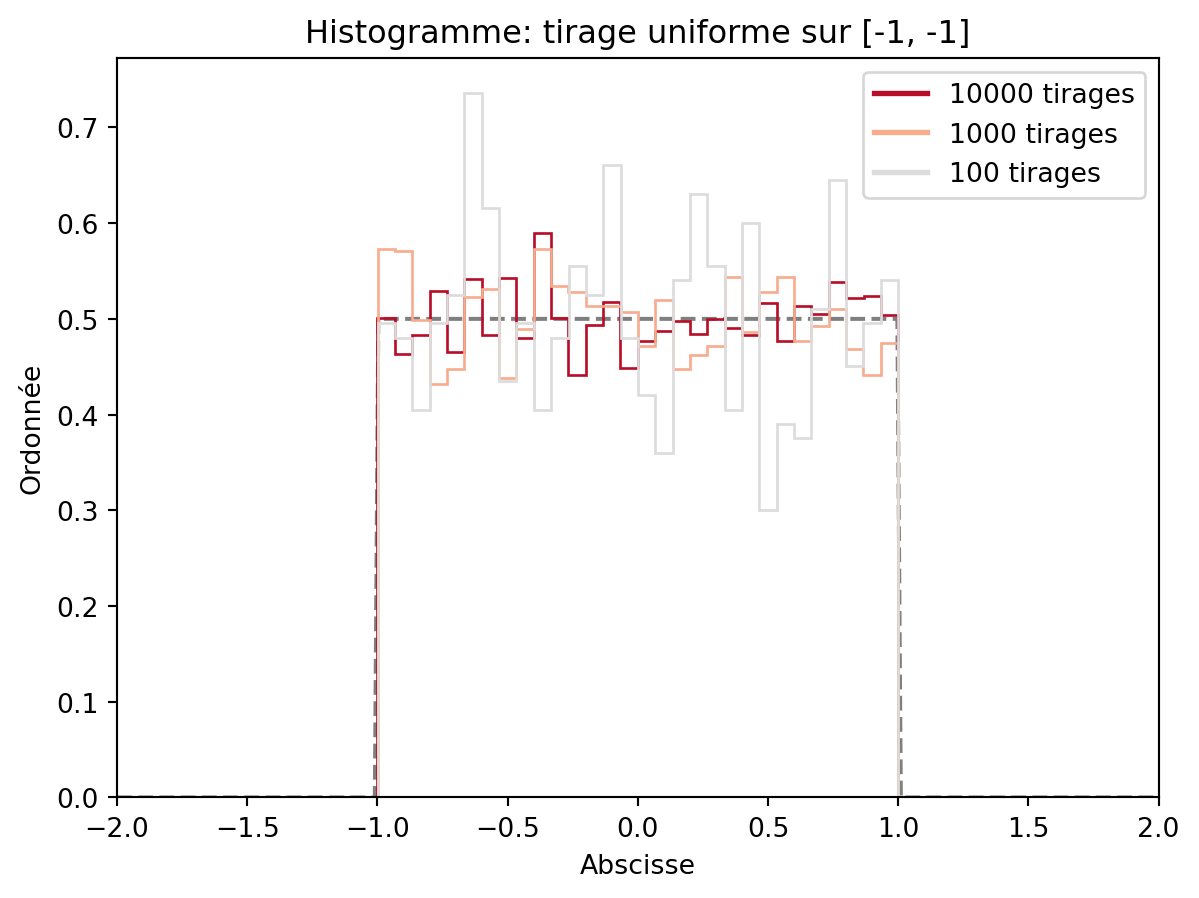

Attention quand vous tracez des histogrammes pour des réalisation de la v.a. non bornées: pour la gaussienne, les histogrammes sont bons

Solution

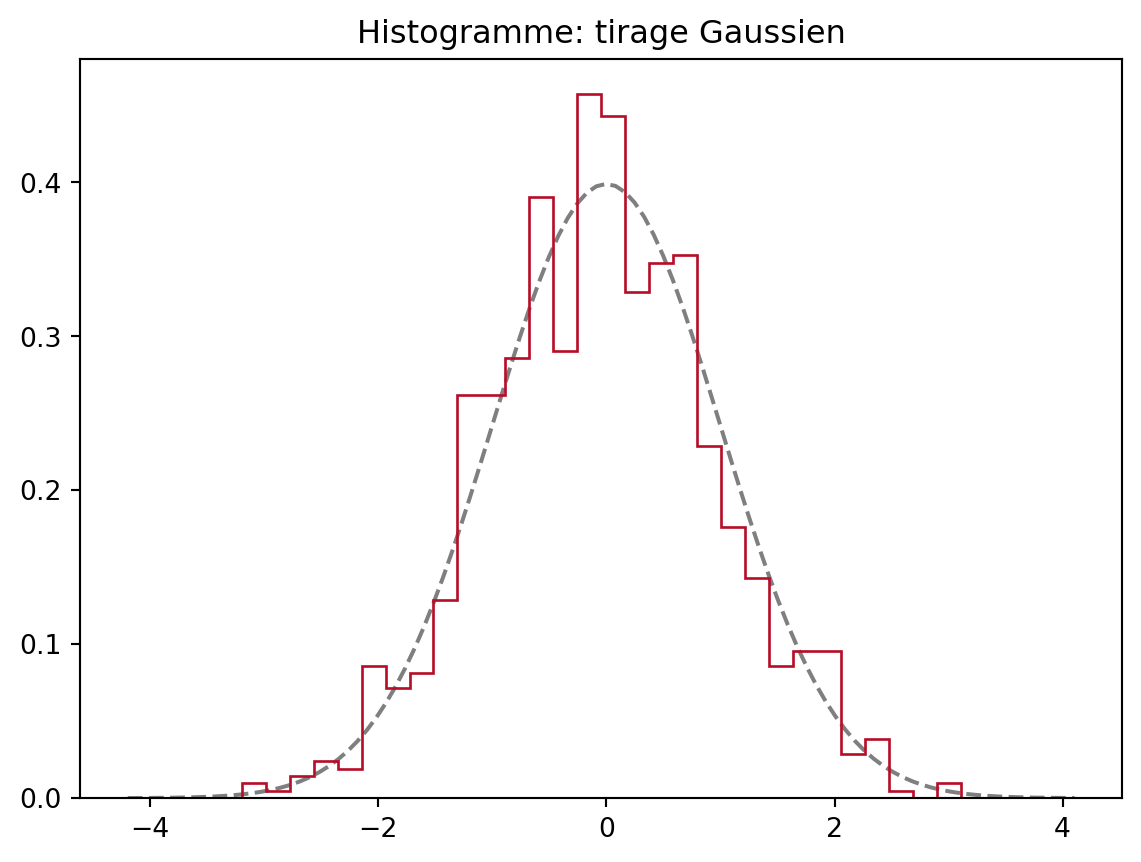
vectGauss = np.random.randn(1000)

fig, ax = plt.subplots()

xx = np.linspace(vectGauss.min() - 1, vectGauss.max() + 1, 100)
ax.plot(xx, stats.norm.pdf(xx, loc=0, scale=1),'--', color='k', label="Loi théorique", alpha=0.5)

ax.hist(vectGauss, histtype='step', density=True, bins=30, label="Histogramme 10000", fill=False, color=colors[0])
# plot density

plt.title('Histogramme: tirage Gaussien')
plt.show()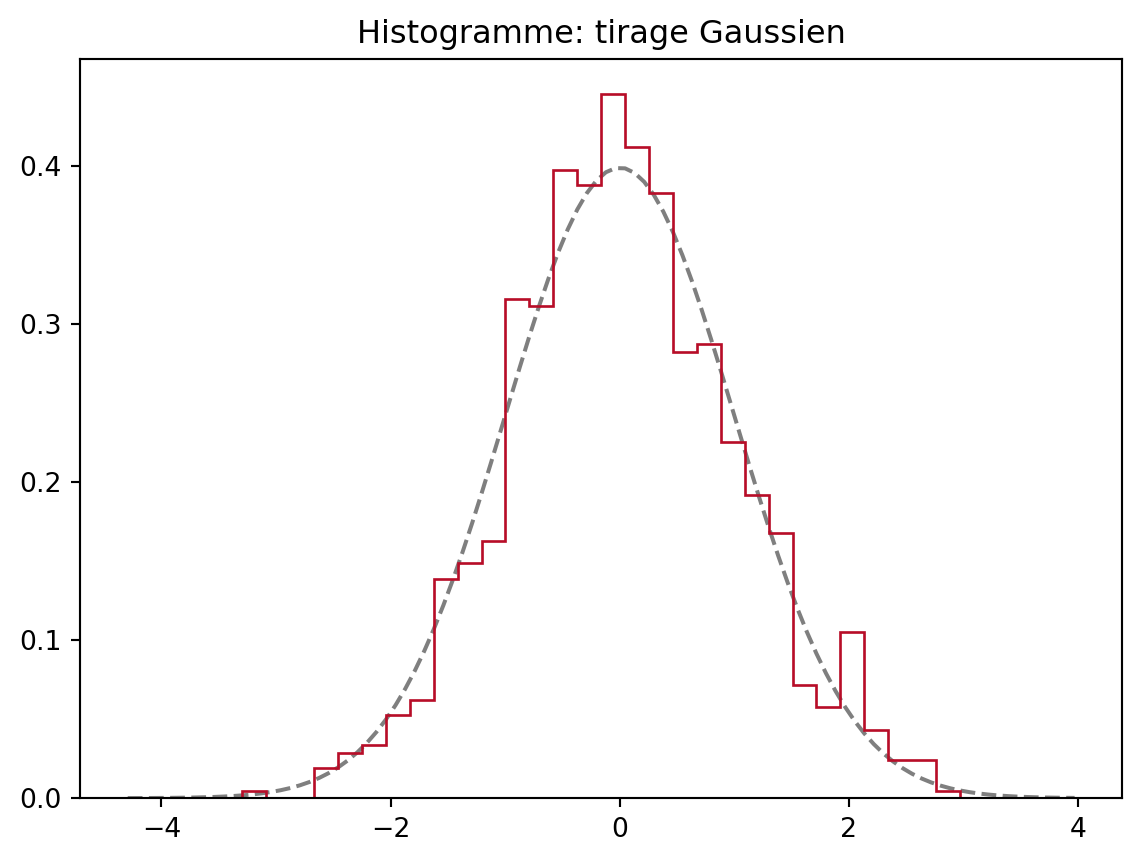

Pour la Cauchy, les histogrammes se comportent mal

Solution

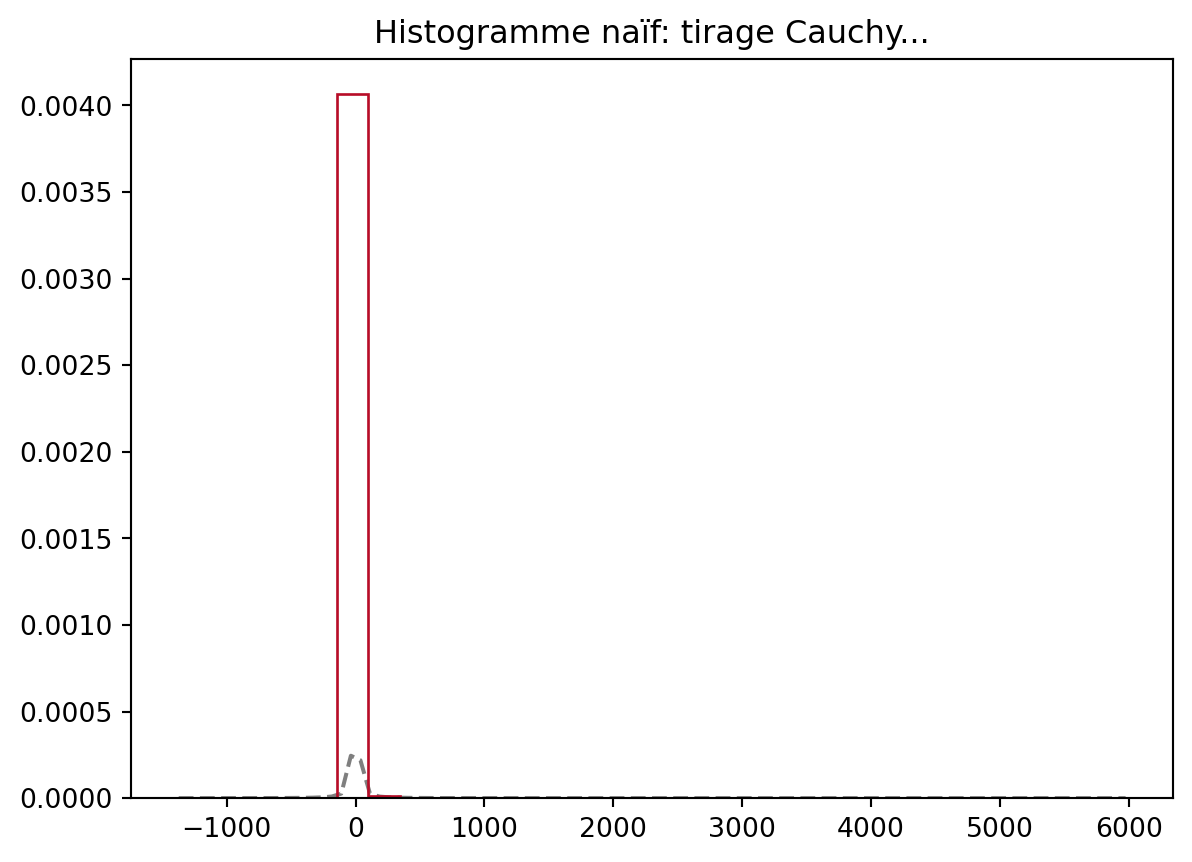
vectCauchy = np.random.standard_cauchy(10000)

fig, ax = plt.subplots()

xx = np.linspace(vectCauchy.min() - 1, vectCauchy.max() + 1, 100)
ax.plot(xx, stats.cauchy.pdf(xx, loc=0, scale=1),'--', color='k', label="Loi théorique", alpha=0.5)

ax.hist(vectCauchy, histtype='step', density=True, bins=30, label="Histogramme 10000", fill=False, color=colors[0])
plt.title('Histogramme naïf: tirage Cauchy...')
plt.show()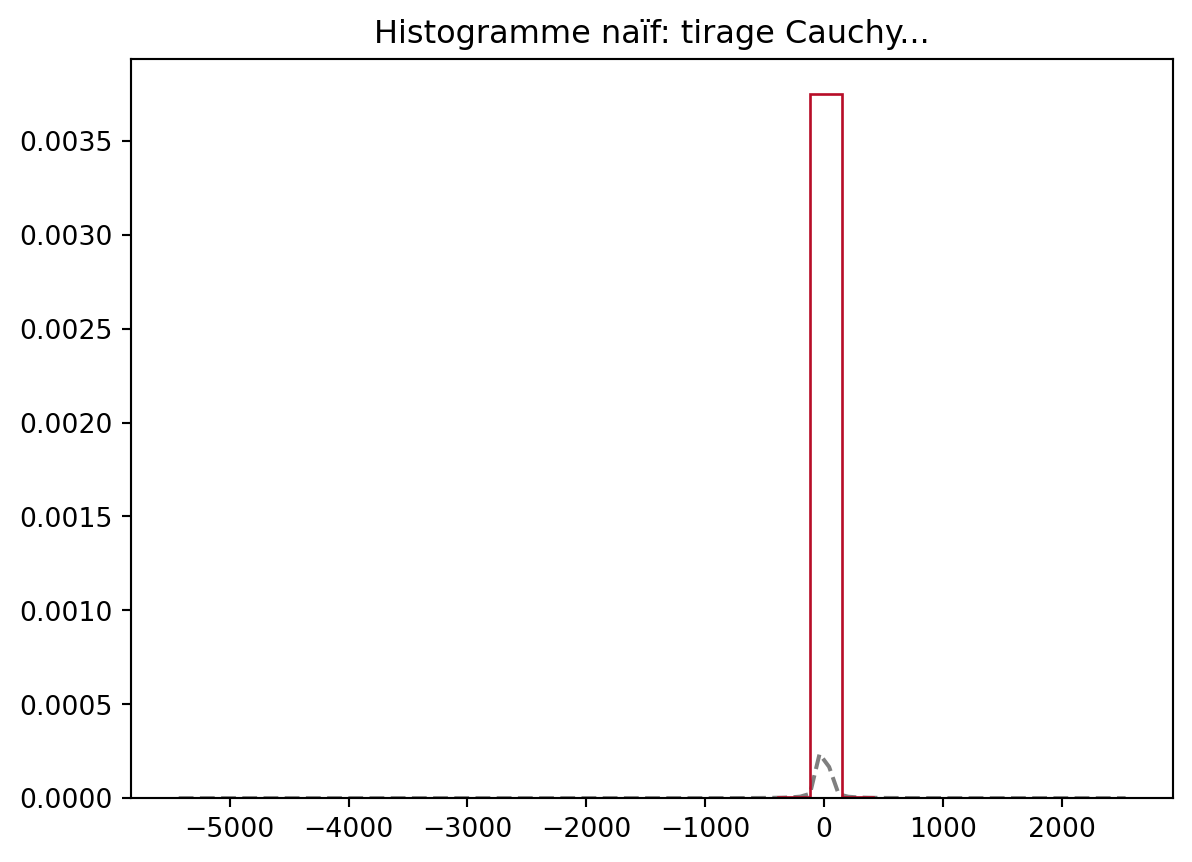

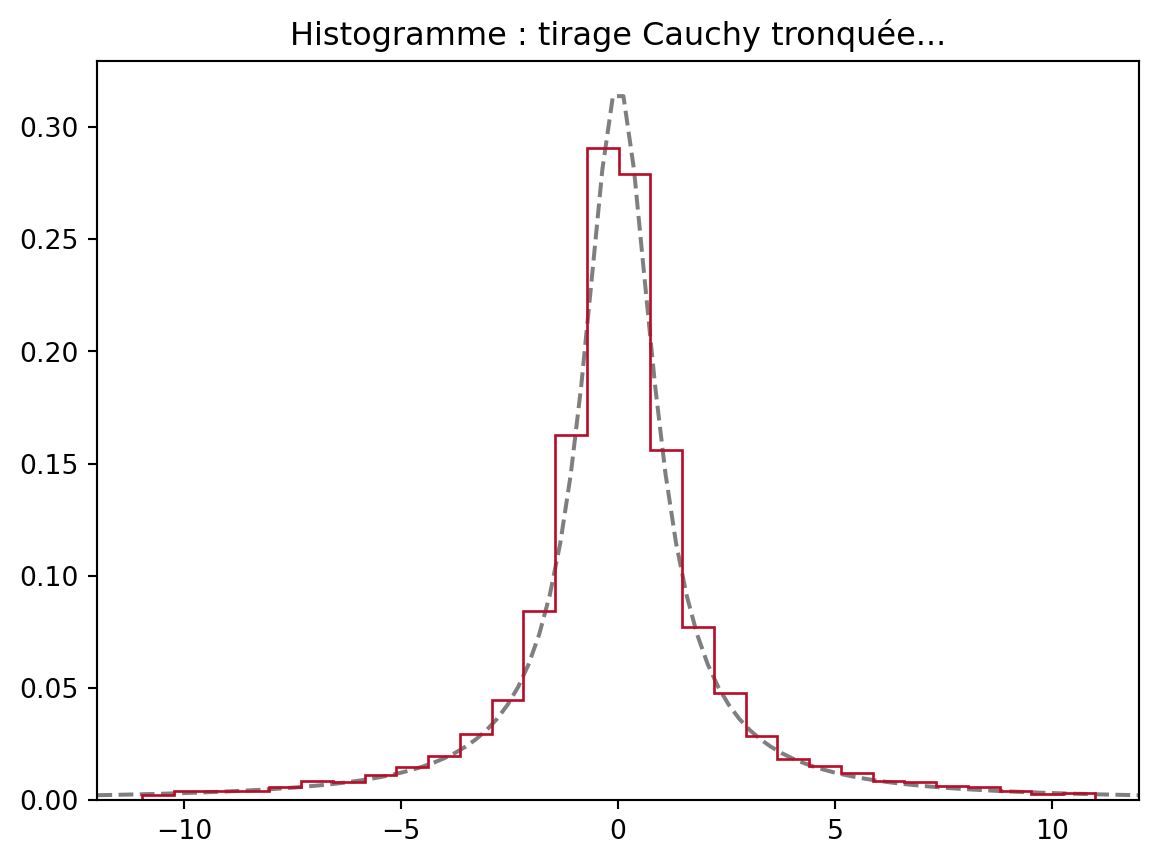
Il faut tronquer (ci-dessous entre -11 et 11) pour retrouver une représentation fidèle:

Solution

xmax = 11
fig, ax = plt.subplots()

xx = np.linspace(-xmax - 1, xmax + 1, 100)
ax.plot(xx, stats.cauchy.pdf(xx, loc=0, scale=1),'--', color='k', label="Loi théorique", alpha=0.5)

ax.hist(vectCauchy[np.abs(vectCauchy) < xmax], histtype='step', density=True, bins=30, label="Histogramme 10000", fill=False, color=colors[0])

ax.set_xlim((-xmax - 1, xmax + 1))

plt.title('Histogramme : tirage Cauchy tronquée...')
plt.show()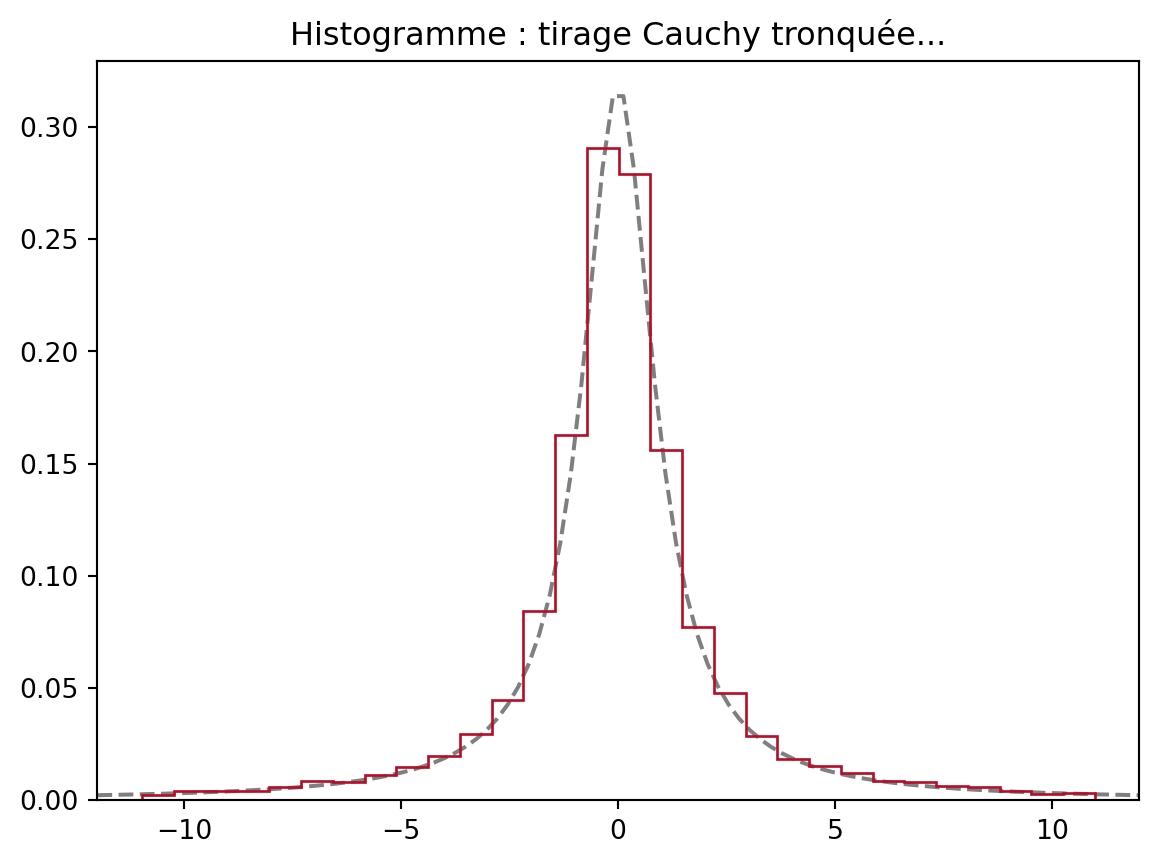

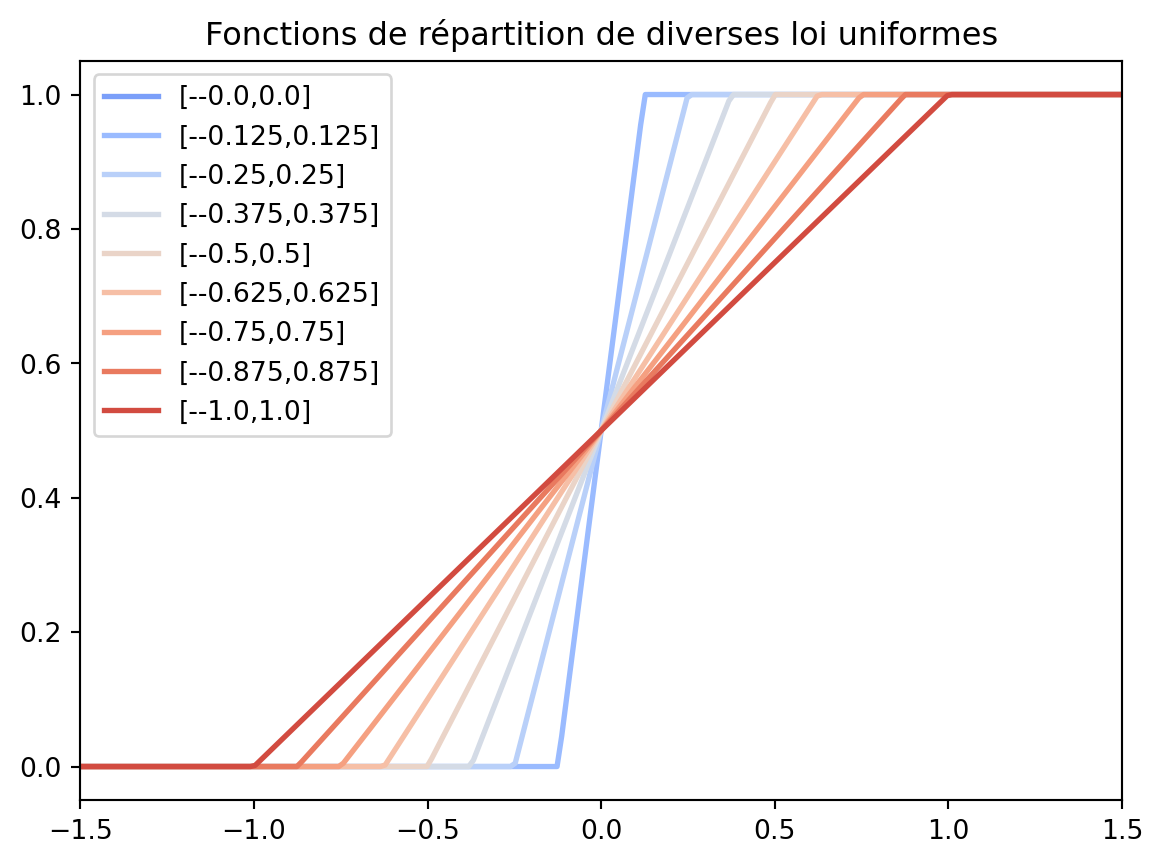
Exercice 2: Fonction de répartition de la loi uniforme

La fonction de répartition de la loi uniforme est obtenue via la commande cdf du module scipy.stats.uniform. À l’aide de la commande plt.plot tracez en bleu la fonction de répartition de la loi uniforme sur [-1,1], [-0.7, 0.7] et [-0.5,0.5] et donnez un titre à votre graphique.

  • On contrôle avec lw (linewidth) l’épaisseur du trait.
  • Vous pouvez modifier le style et les marqueurs facilement en matplotlib. Une liste exhaustive est donnée ici: matplotlib.pyplot.plot.html
  • Enfin pour les couleurs on pourra consulter l’aide en ligne ici: Color tutorial. La manière la plus simple est souvent d’ajouter l’option color=nom_couleur dans la fonction plot.

Manipulez les différentes options pour vous familiariser avec les graphes

Pour aller plus loin

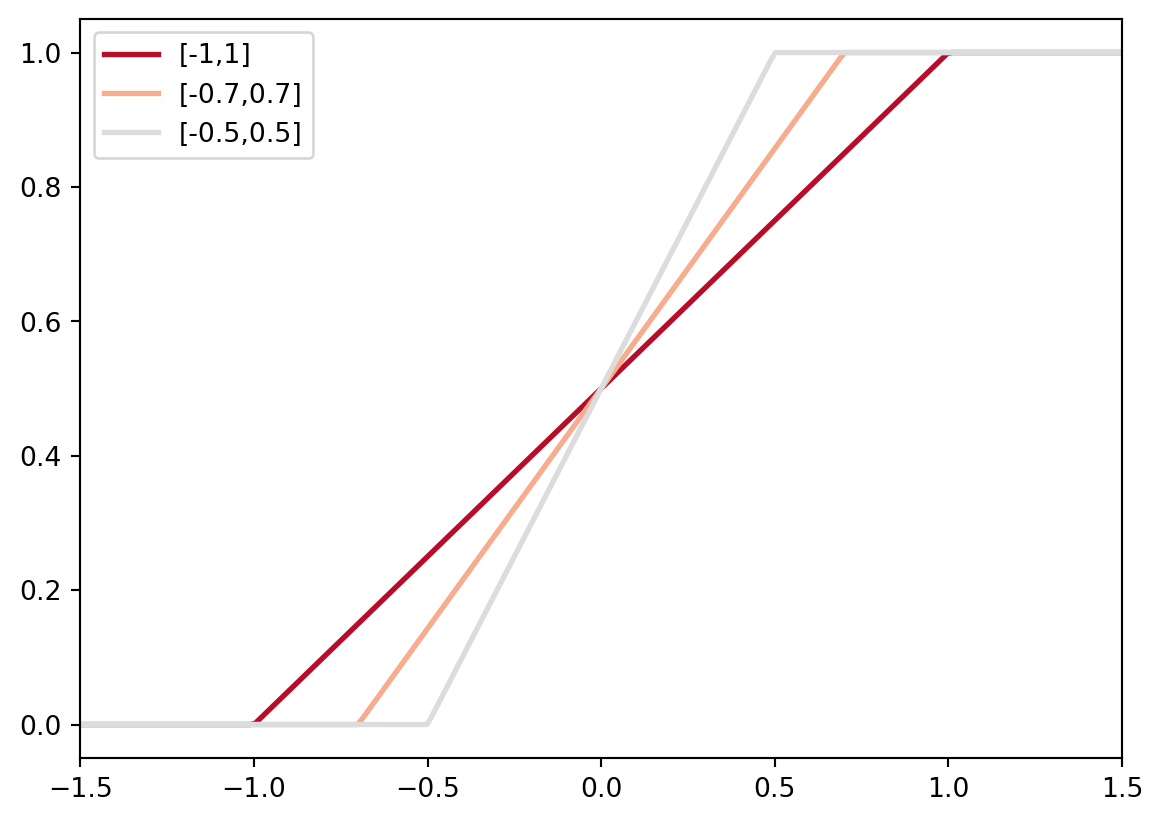
Tenter de reproduire la figure suivante

Solution

fig, ax = plt.subplots()
lines = np.linspace(0, 1, 9)

for i, vali in enumerate(lines):
    ax.plot(x, stats.uniform.cdf(x, loc=-vali,scale=2*vali), color=cmap(0.2+0.8*i/len(lines)), label=f"[-{-vali},{-vali+2*vali}]", lw=2)

ax.set_xlim([-1.5,1.5])
plt.legend()
plt.title("Fonctions de répartition de diverses loi uniformes")
plt.show()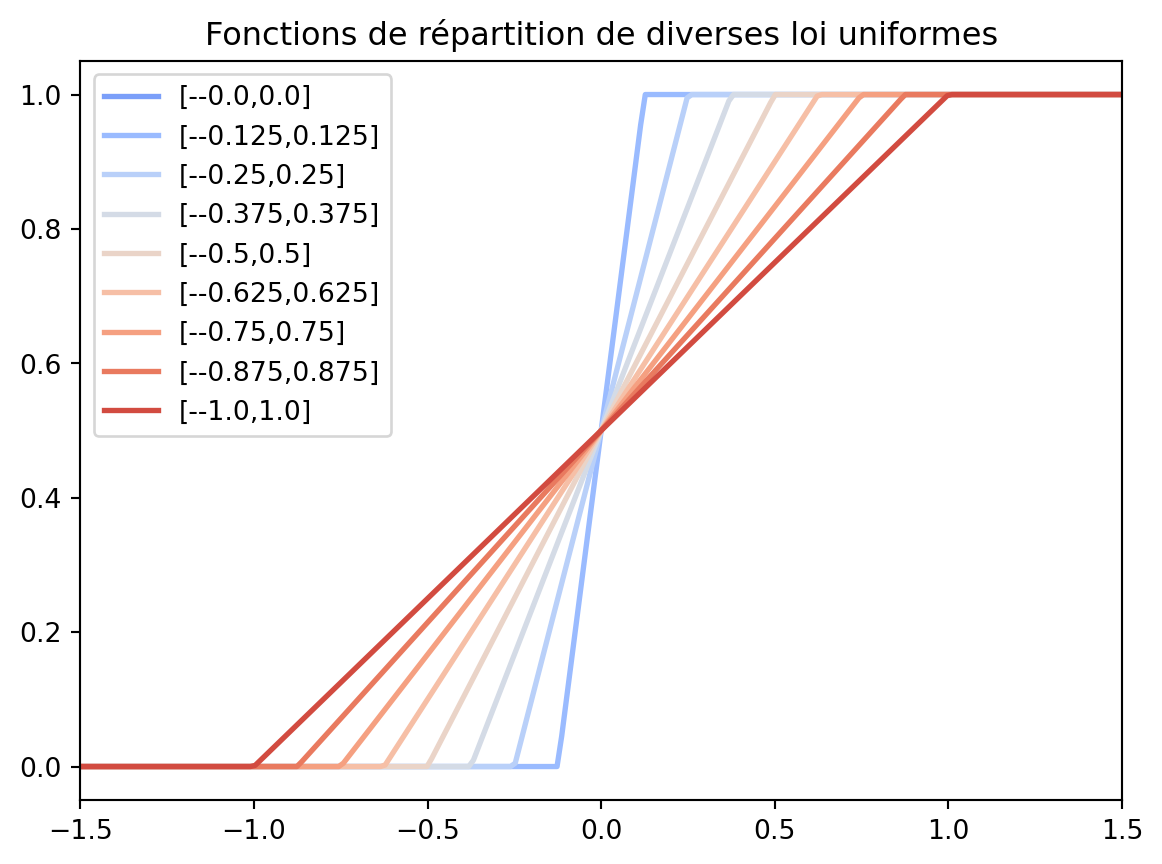

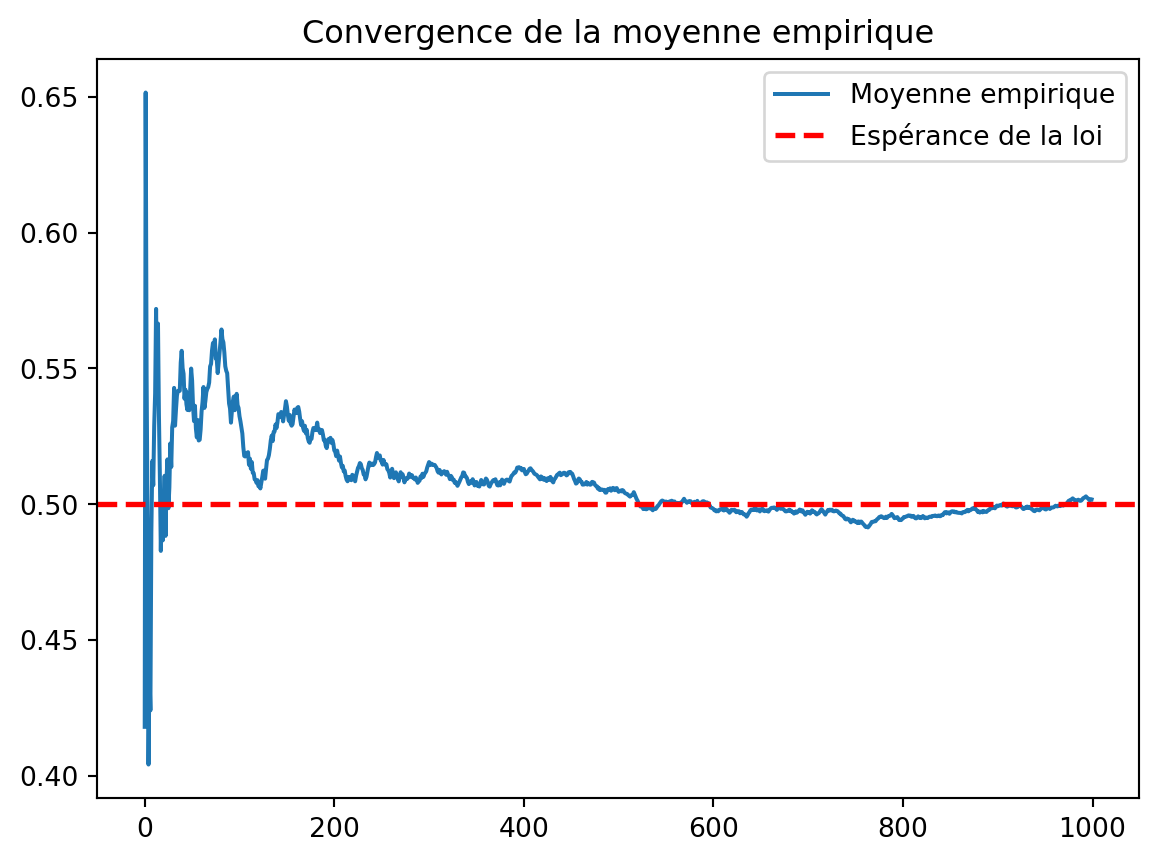
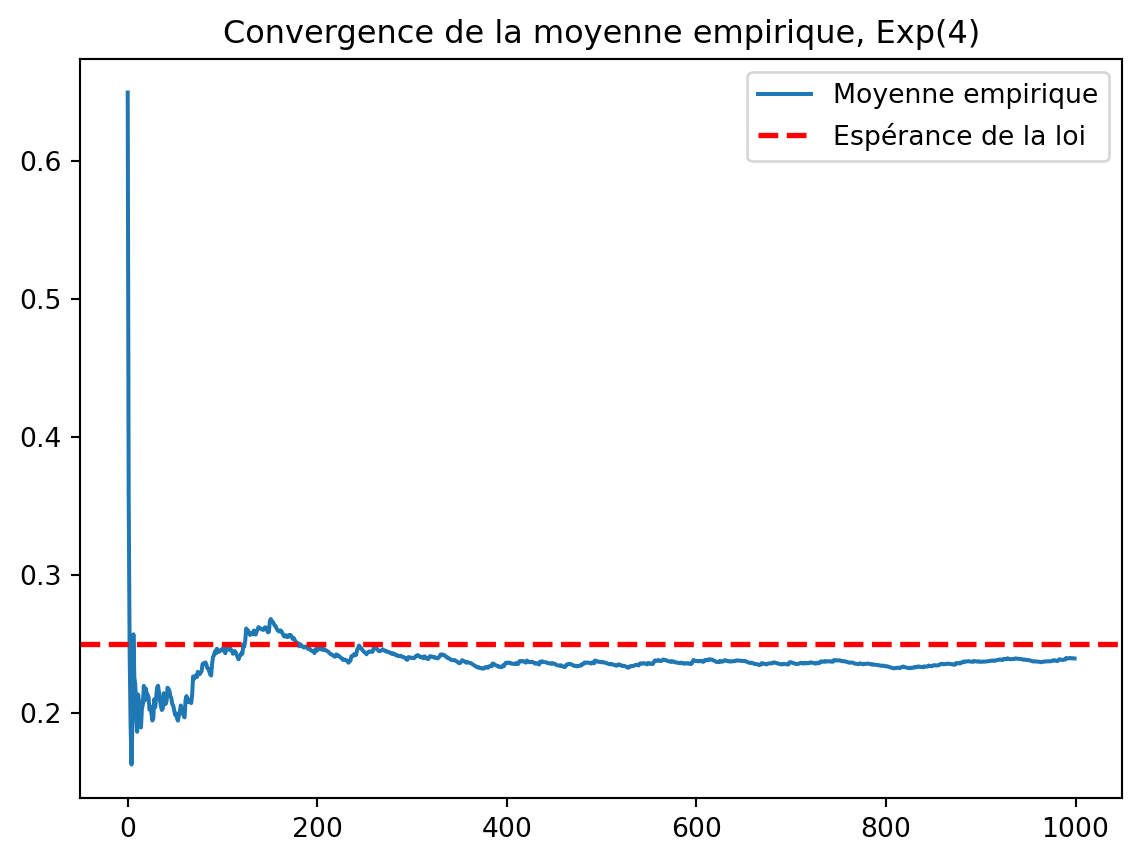
Exercice 3: Étude de la moyenne empirique

Créez un vecteur de taille 100 composé de réalisations i.i.d. de variables uniformes sur [0,1]. Calculez dans un vecteur la moyenne cumulée des valeurs générées. Représenter graphiquement l’évolution de ces moyennes. Vers quoi semble converger la moyenne quand la taille de l’échantillon augmente ?

Pour ajouter une droite à un graphe, on utilise la commande ax.axhline. Ajoutez en rouge la droite d’équation y=1/2 sur le graphe précédent. Refaites cet exercice avec un échantillon de taille n=1000 pour observer plus finement la convergence.

Solution

vect = rng.uniform(0, 1, 1000)

fig, ax = plt.subplots()
ax.plot(np.cumsum(vect) / np.arange(1, len(vect)+1), label="Moyenne empirique")
ax.axhline(0.5, linestyle="--", color='red', lw=2, label="Espérance de la loi")
ax.set_title("Convergence de la moyenne empirique")
plt.legend()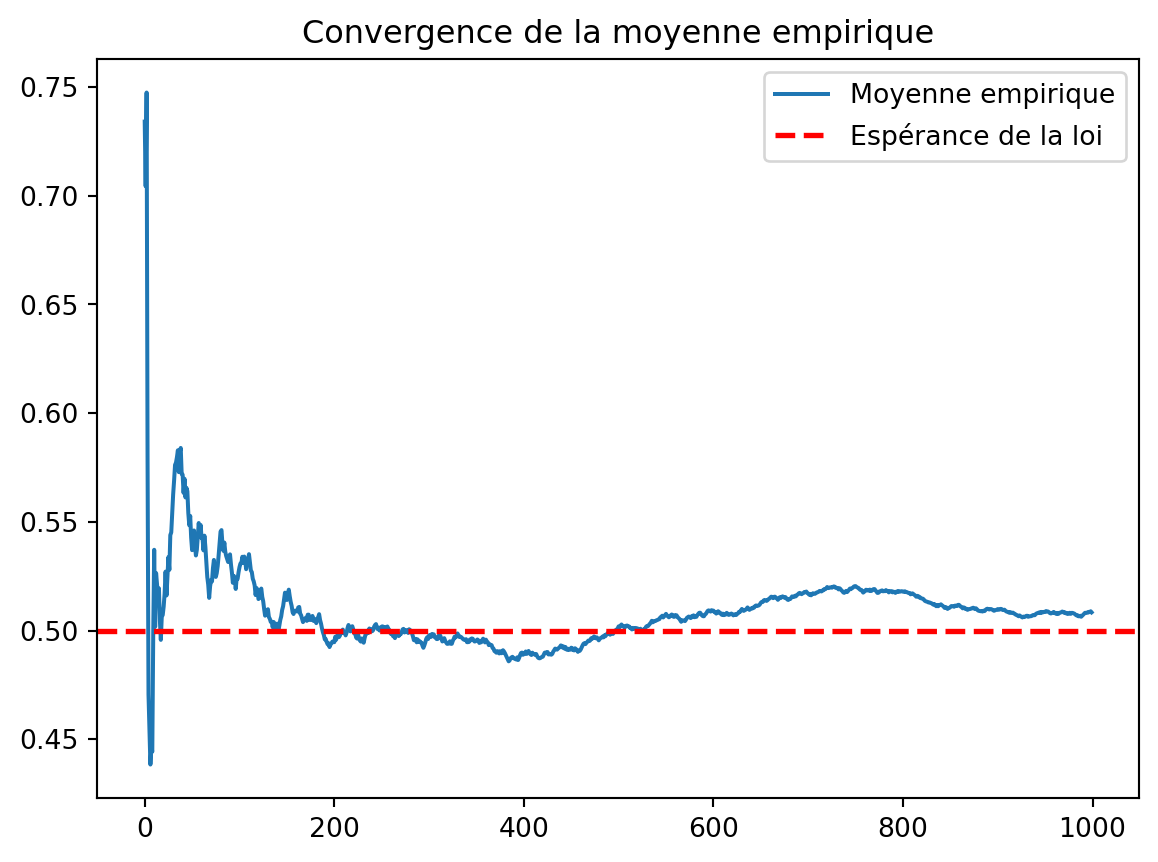

Exercice 4: Méthode d’inversion, loi exponentielle et loi de Cauchy

  • Représentez graphiquement la fonction de répartition d’une loi exponentielle de paramètre \lambda=1.
  • Écrivez une fonction dzexpo qui prend en argument une taille d’échantillon n et un paramètre \lambda > 0 et qui donne en sortie un échantillon de taille n de loi \mathcal{E}(\lambda). On utilisera la méthode d’inversion vue en cours et seulement des tirages uniformes sur [0,1]. Attention, le mot clef lambda est un mot réservé en Python.
  • Représentez graphiquement l’histogramme cumulé (voir l’option cumulative de hist) d’un tel échantillon pour n=10^2, n=10^3, puis n=10^4, et pour \lambda = 1, puis \lambda = 4. Superposez à chaque fois le graphe de la fonction de répartition de \mathcal{E}(\lambda).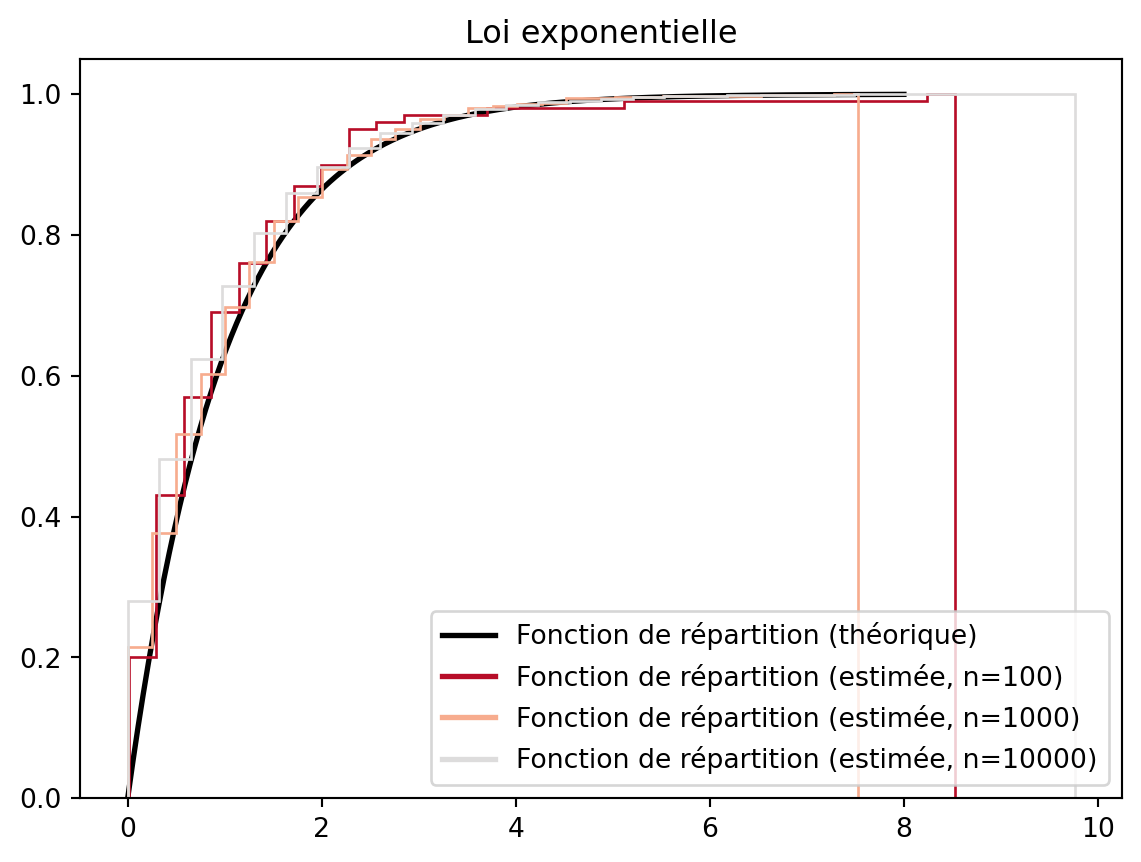
  • Illustrez graphiquement la loi des grands nombres avec \lambda = 1, puis \lambda = 4. On tracera en particulier la droite d’équation y=\mathbb{E}[X], où X \sim \mathcal{E}(\lambda).
  • Reprenez les questions précédentes avec la loi de Cauchy (mais représenter la densité plutôt que les fonctions de répartition). Commentez les résultats obtenus.

Solution

fig, ax = plt.subplots()
x = np.linspace(0, 8, num=300)
ax.plot(x, stats.expon.cdf(x, scale=1), color='k', label="Fonction de répartition", lw=2)


def dzexpo(n, lbd):
    U = rng.uniform(size=n)
    return - np.log(U) / lbd

ax.hist(dzexpo(100, 1), density=True,  cumulative=True, histtype='step',bins=30, label="Estimation de la fonction de répartition", color=colors[0])
ax.hist(dzexpo(1000, 1), density=True,  cumulative=True, histtype='step',bins=30, label="Estimation de la fonction de répartition", color=colors[1])
ax.hist(dzexpo(10000, 1), density=True,  cumulative=True, histtype='step',bins=30, label="Estimation de la fonction de répartition", color=colors[2])
ax.set_title("Loi exponentielle")

custom_lines = [Line2D([0], [0], color='k', lw=2),
                Line2D([0], [0], color=colors[0], lw=2),
                Line2D([0], [0], color=colors[1], lw=2),
                Line2D([0], [0], color=colors[2], lw=2),
                ]

ax.legend(custom_lines,
          ['Fonction de répartition (théorique)',
          'Fonction de répartition (estimée, n=100)',
          'Fonction de répartition (estimée, n=1000)',
          'Fonction de répartition (estimée, n=10000)',
          ], loc='lower right')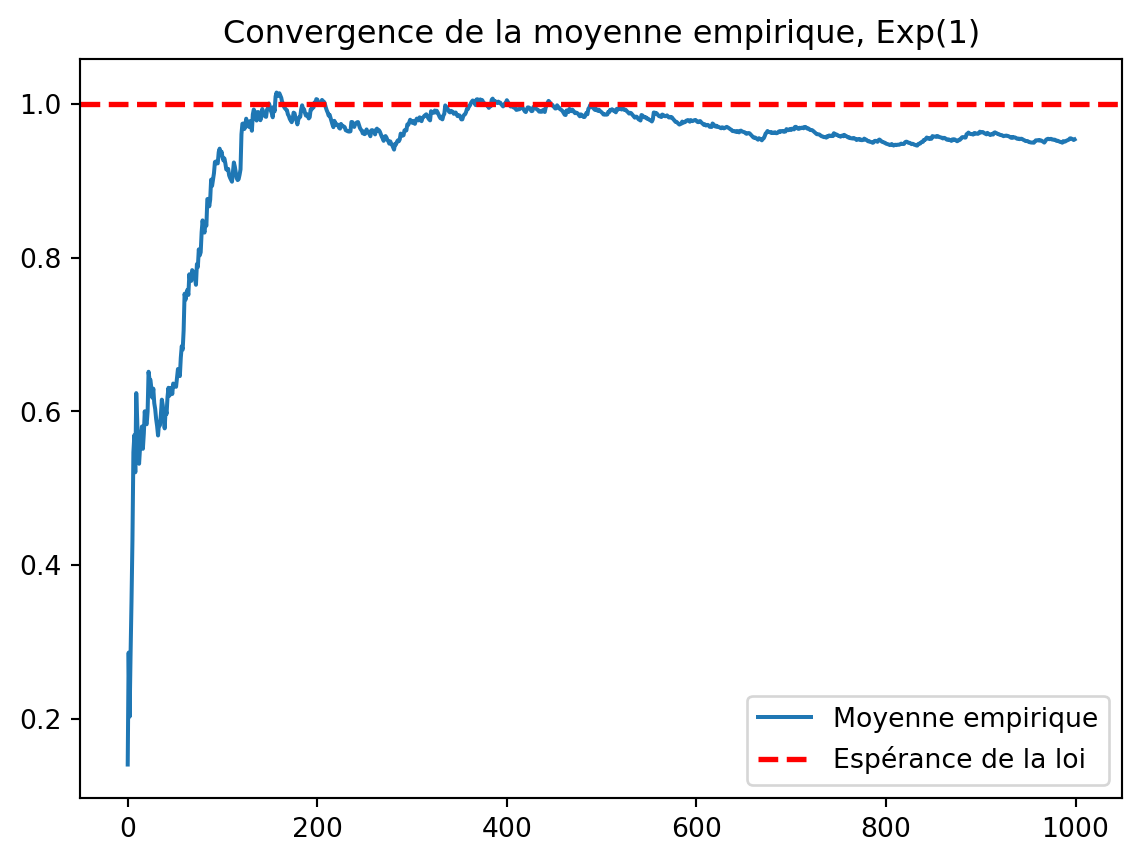

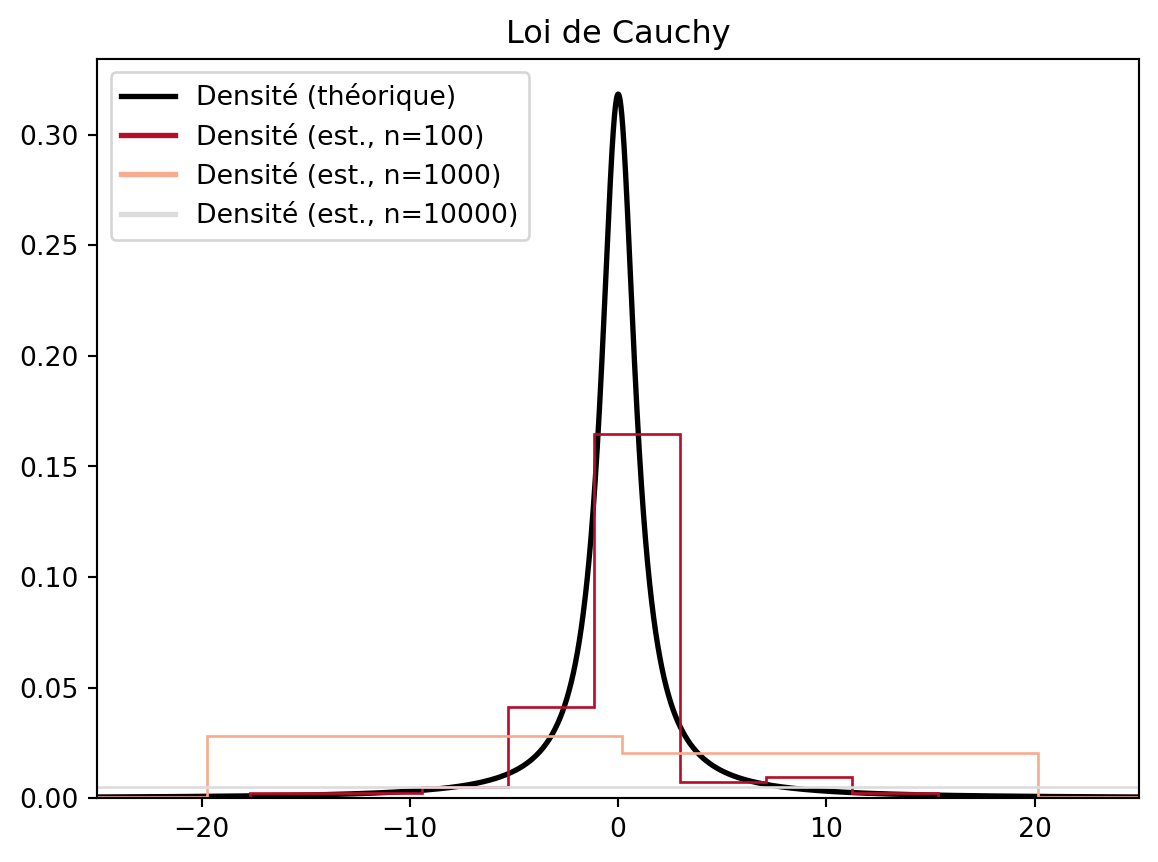
On reprend le tout avec la loi de Cauchy:

Solution

vect = dzcauchy(1000)
fig, ax = plt.subplots()
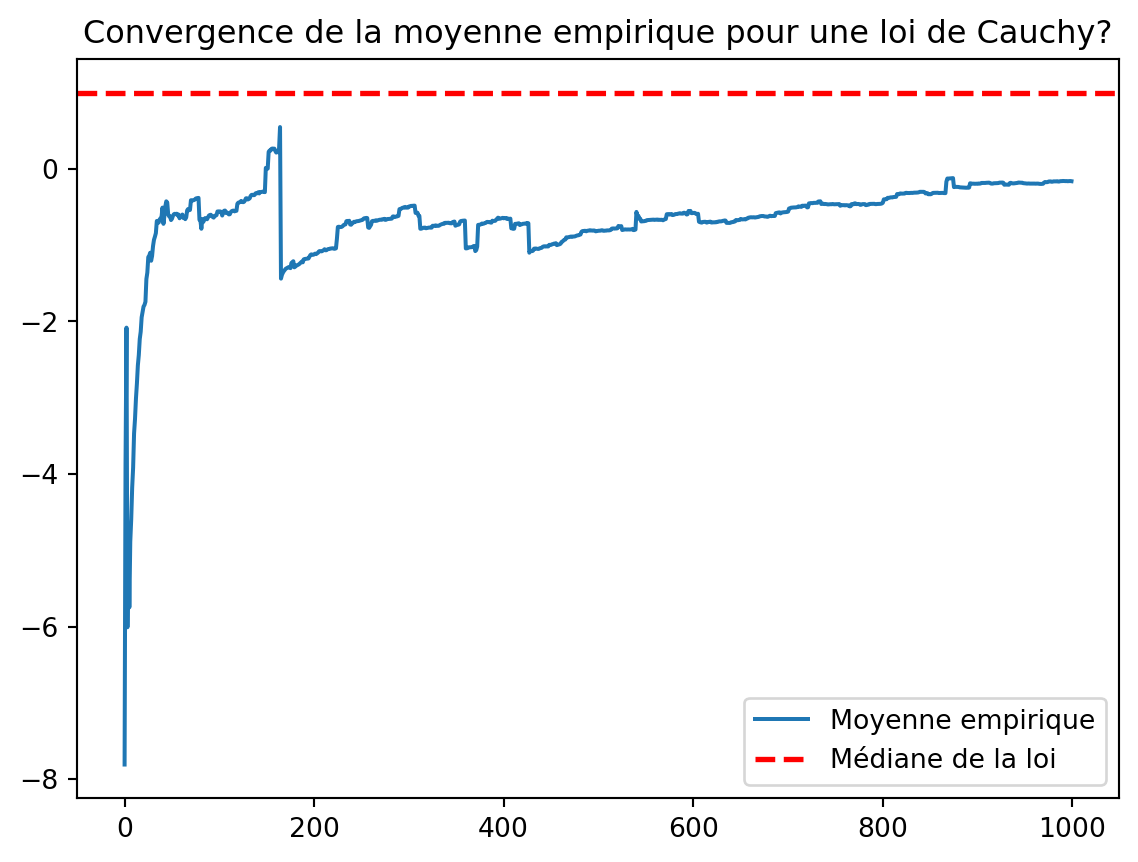
ax.plot(np.cumsum(vect) / np.arange(1, len(vect)+1), label="Moyenne empirique")
ax.axhline(1, linestyle="--", color='red', lw=2, label="Médiane de la loi")
ax.set_title("Convergence de la moyenne empirique pour une loi de Cauchy?")
plt.legend()

Pour aller plus loin: les méthodes à noyaux (KDE)

Le phénomène qui apparaît avec la loi de Cauchy est le suivant: les queues de la loi de Cauchy sont tellement épaisses que l’écart entre \min_i(X_i) et le \max_i(X_i) (les X_i étant les tirages effectués) est du même ordre de grandeur que le nombre de tirages, n. Comme la fonction hist discrétise l’intervalle [\min(X_i), \max(X_i)] en le nombre de boîtes (bins) on observe peu de points dans chaque boîte ce qui rend l’estimation de la densité trop petite.

Ce point n’est pas un problème pour les lois gaussiennes, car la largeur de l’intervalle [\min(X_i), \max(X_i)] est de l’ordre de \sqrt{\log(n)}, et comme on a n points à placer dans cet intervalle, il y a assez de points dans chaque boîte pour obtenir une bonne estimation.

Notons que les méthodes à noyaux (KDE) ne souffrent pas de ce défaut, car les “boîtes” sont en fait centrées autour des données et non sur une grille préalablement fixée comme c’est le cas pour l’histogramme. Voir par exemple l’aide de scikit learn ou encore wikipedia, méthode à noyau.

import plotly.graph_objects as go
from sklearn.neighbors import KernelDensity
n_sample = 1000
x = np.linspace(-2, 10, num=10000)
X=dzcauchy(n_sample)

kde = KernelDensity(kernel="tophat", bandwidth=0.1).fit(X.reshape(-1, 1))
log_dens = kde.score_samples(x.reshape(-1, 1))
fig=go.Figure()

fig.add_trace(go.Scatter(x=x, y=np.exp(log_dens), mode='lines', line=dict(color='blue', width=2), name="Estimation de la densité"))
fig.add_trace(go.Scatter(x=x, y=stats.cauchy.pdf(x, scale=1, loc=0), mode='lines', opacity=0.6, line=dict(color='black', width=2), name="Densité de Cauchy"))

fig.update_layout(
    template="simple_white",
    showlegend=True,
)
print(f"Taille de l'échantillon: {n_sample}")
print(f"Étendue: {np.max(X)-np.min(X)}")
Taille de l'échantillon: 1000
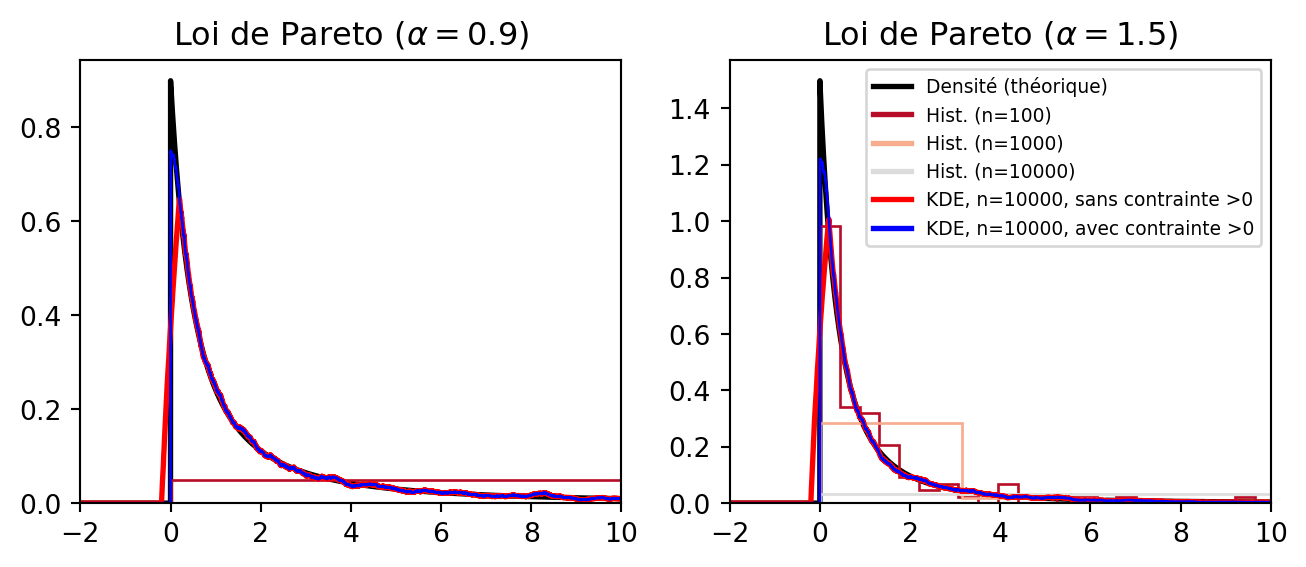
Étendue: 1488.6440039526083

Notons qu’un phénomène similaire apparaît aussi avec la loi de Pareto, qui est aussi une loi à queue lourde quand son paramètre \alpha est plus petit que 1.

Taille de l'échantillon: 1000
Étendue: 8254.628995163406
Taille de l'échantillon: 1000
Étendue: 152.94757156399794

Retour au sommet